玩玩算法 菜死了 大概记录一下我的弃坑过程吧((
简单一点的题目
小凡一次可以爬1或2阶楼梯, 现在一共有n阶楼梯, 求一共有多少种上楼方式?
我的想法
第一次看的时候 由于上楼必定是由上一阶和两阶组成的, 我想遍历0~n来决定上多少个一阶, n减去来得到一次上2阶的次数 再用 C(高中学的组合) 相乘, 就能得到最后的结果
一般解法
听说这叫递推
由于最后一次上楼梯必定为上一阶或者上两阶
就可以把上楼梯分为两段
如对于上3阶楼梯, 可以是先上1阶再上2阶 或者先上2阶再上1阶, 总共两种方式
对于上4阶楼梯, 是先上2阶再上2阶 或者先上3阶再上1阶
而由于上3阶在上一步已经算出来了… 上四阶就是上2阶的方式总数+上3阶的总数
对于上n阶楼梯, 是先上n-2阶再上2阶 或者先上n-1阶再上1阶… F(n) = F(n-1) + F(n-2)
稍微扩展一点
对于1037:
楼梯有n阶,小凡腿长,他每步最多能上3阶楼梯,他很笨,想知道他有多少种上到第n阶楼梯的方式。你能帮帮他吗?
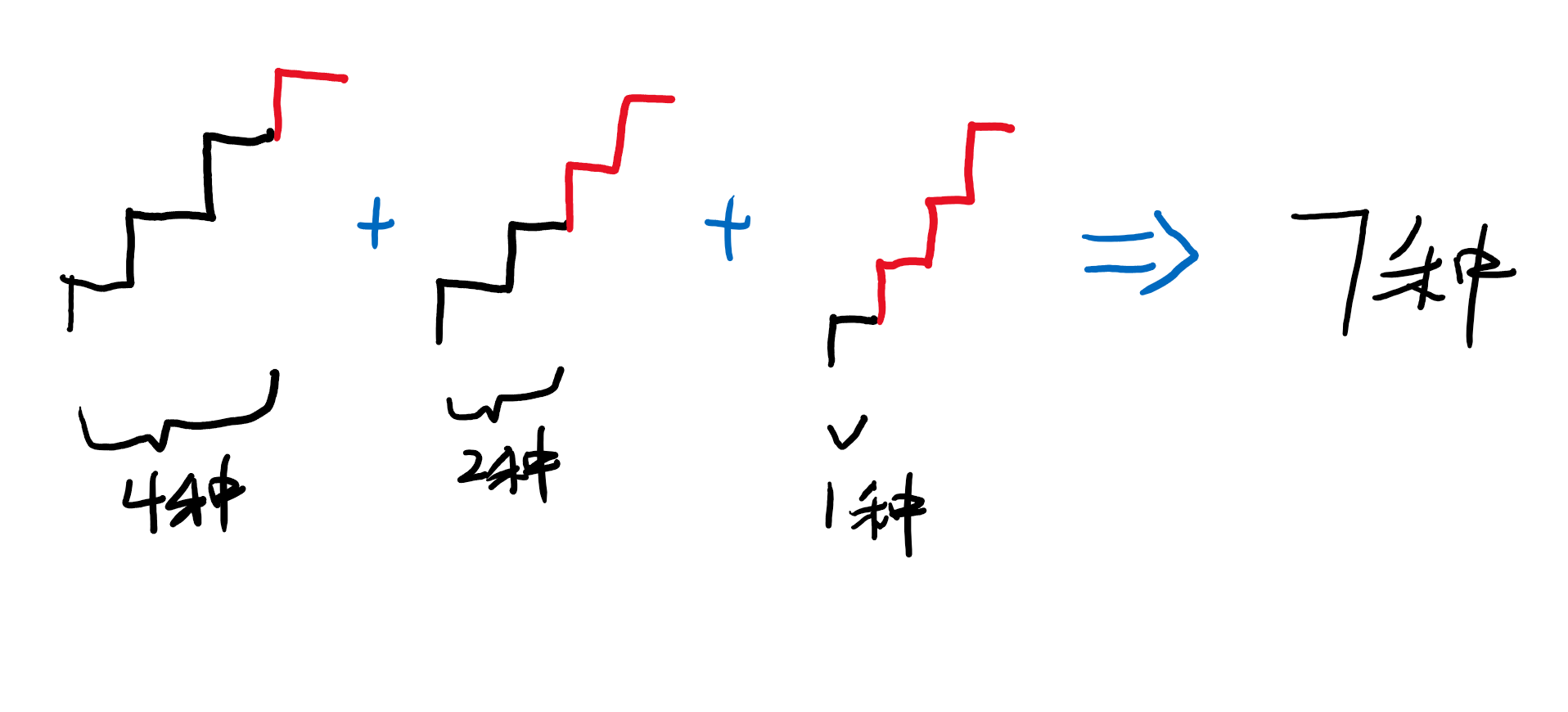
F(n) = F(n-1) + F(n-2) + F(n-3) 而这道题吧.. 如果你直接写递归
1
2
3
4
5
6
7
8
9
// 爬爬爬 我最会爬了
long long pa(int floors)
{
if (floors == 1) { return 1; }
if (floors == 2) { return 2; }
if (floors == 3) { return 4; }
return pa(floors-1) + pa(floors-2) + pa(floors-3);
}
对于题目的floors输入最大可以到50层 我电脑差不多在30层就卡死了 那可以用个数组缓存一下结果(同一层只用算一次呗) 或者直接打表((